OKCJUG Lightning Talks

This month, we will have lightning presentations... 5 minutes and 20 slides set on auto-timer. I'll do some TDD and ScalaCheck directly through powerpoint! Get it here.

ScalaCheck is Neat-o!

ScalaCheck is a testing library for Scala (and Java!). It is a step beyond just writing tests, you actually assert properties of some code and it generates a number of tests dynamically to test it.

A recent example of using this came from this StackOverflow question. It required a largish number of test cases, so it seemed a perfect fit to try out ScalaCheck.

The code to test was:

package blevins.example

object BigIntEncoder {
  val radix = 36
  
  implicit def byteArrayToString(ba: Array[Byte]): String = {
    new java.math.BigInteger(ba).toString(radix)
  }
  
  implicit def stringToByteArray(s: String): Array[Byte] = {
    new java.math.BigInteger(s, radix).toByteArray
  }
  
}

To test, you write something like this:

package blevins.example

import org.scalacheck._

object BigIntEncoderSpecification extends Properties("BigIntEncoder") {
  import Prop._
  import Gen._
  
  def genArray( fill: Array[Byte] => Unit) = Gen.sized { size => 
    val bytes: Array[Byte] = new Array[Byte](size)
    fill(bytes)
    bytes
  } suchThat (_.size > 0)

  def filledByteArray( i: int ) = genArray(bytes =>
    for (i <- 0 to bytes.length - 1) { bytes(i) = i.asInstanceOf[Byte] }
  )
  
  val arbByteArray = genArray(bytes => scala.util.Random.nextBytes(bytes))

  val zeroByteArray = filledByteArray( 0x00 )
  
  val fullByteArray = filledByteArray( 0xff )
  
  def checkEncodingRoundTrip = { (ba: Array[Byte]) => 
    import BigIntEncoder._
    ba deepEquals stringToByteArray(byteArrayToString(ba))
  }
  
  property("random") = forAll(arbByteArray)(checkEncodingRoundTrip)
  property("zero") = forAll(zeroByteArray)(checkEncodingRoundTrip)
  property("full") = forAll(fullByteArray)(checkEncodingRoundTrip)
}

This code will generate random, all-zero, and all-binary-ones (0xff) arrays and test their equality using the checkEncodingRoundTrip method, which exercises the code to be tested. It failed sometimes for the random array, and failed all the time for the other two types. I also noticed that the random array failed when the first byte of the arrays was either 0x00 or 0xff. I assumed that this was a side effect of BigInteger taking the two-complement of the byte array, so I padded it like so:

package blevins.example

object BigIntEncoder {
  val radix = 36
  
  implicit def byteArrayToString(ba: Array[Byte]): String = {
    new java.math.BigInteger(addByte(ba)).toString(radix)
  }
  
  implicit def stringToByteArray(s: String): Array[Byte] = {
    stripByte(new java.math.BigInteger(s, radix).toByteArray)
  }
  
  def addByte(ba: Array[Byte]): Array[Byte] = {
    val h = new Array[Byte](1)
    h(0) = 0x01
    h ++ ba
  }
  
  def stripByte(ba: Array[Byte]): Array[Byte] = {
    ba.slice(1,ba.size)
  }
  
}

This produced the desired results (all passing), but a large amount of output. I wrote my own output-generator like this:

package blevins.example

object Test extends Application {
  import org.scalacheck._
  import org.scalacheck.Test._
  
  val params = Params(5000, 10, 1, 100, new java.util.Random(), 1, 1)
  val props = checkProperties(BigIntEncoderSpecification, params)
  for ((name, result) <- props) {
    println(name + ": " + result.status)
  }

}

This also increased the number of tests-per-property from 100 to 5000.
My output was:

BigIntEncoder.random: Passed
BigIntEncoder.zero: Passed
BigIntEncoder.full: Passed

Yay! Now go watch TV.

Reflective Calls in Scala

Scala 2.8 contains two experimental features to reflectively invoke methods. Are these cool?

  import scala.reflect.RichClass._
  
  val hello = "hello"   
  val helloStartsWith = classOf[String].reflectiveCall(hello, "startsWith")
  val b1: Boolean = helloStartsWith("hell")
  val b2: String = helloStartsWith("heaven") // ClassCastException (Boolean->String)
  val b3 = helloStartsWith("blah") // ClassCastException (Boolean->Nothing)
  
  
  import scala.reflect.Invocation._
  
  val team: AnyRef = "team"
  val any = team o 'contains("I") // returns 'Any'
  val b4: Boolean = team oo 'contains("I") // ok
  val b5 = team oo 'contain("I") // ClassCastException (Boolean->Nothing)
  

The methods called using "o" return "Any". Both reflectiveCall(...) and the "oo" version return the inferred type. Note that this doesn't relieve you from knowing the expected result type, or further reflecting it and casting. This is shown in the runtime errors with b2, b3, and b5.

EDIT: This post was accurate for the nightly 2.8 release when it was written, but this code appears to have been removed from the latest 2.8 betas.

BOM Differences

Sometimes it helps me think about my work if I write it out on virtual paper. So, be warned that this post will probably not be very entertaining or educational. But, I do promise that there is an obscure reference to the movie "Kung-Fu Panda" hidden within.

Here's an interesting project I'm working on. The goal of the project is to effectively visualize the differences between two Bills of Materials (BOMs) from our ERP system. For those unfamiliar with BOMs, they are just a hierarchical structure of the components that make up a product being manufactured. A real nerd might call it an acyclic, directed, weighted (weights are the quantities) graph. But, it is easier to just think of it as a tree.

Turns out that it is pretty useful to be able to easily see what the differences are between two different bills of materials, especially for people who like to scratch their heads and figure out how to make the product cheaper, or what price to sell it for, or assign costs to products, etc.

The first thought I hatched when thinking about how to implement this was to see how close my needs were to the Java Structure Comparison tool in Eclipse. I have put many hours into driving this particular IDE, and it seems similar to what I wanted.

For those unfamiliar with it, you can take a class that is similar to this:

package com.iecokc.cooking;

public class CakeRecipe {
 public String flour;
 public String eggs;
 public String frosting;
 public void beatEggs() {}
 public void stir() {}
}

And another class like this:

package com.iecokc.baking;

public class CakeRecipe {
 public String flour;
 public String eggs;
 public void beatEggs() {}
 public void stirBriskly() {}
}

and you end up with a navigable tree that shows only the differences, like this:


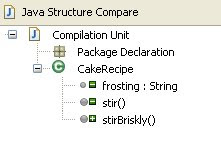
The problem with the comparison implemented in Eclipse is that it uses a strict definition of node identity in the trees that is compares. For example, if I had renamed the one of the classes from "CakeRecipe" to "BundtCakeRecipe", Eclipse would have refused to even consider that these might be similar in structure and therefore should be compared. Nope, different class name or method signature means that it is a completely different thing.

Instead, I needed to have my comparison consider the concept of something being "mostly equal", or "mequal" (trademark pending). If I can pin down this slippery concept of "mequals", I can then make a comparison structure that shows more than just adds and removes, but also edits of a particular node. It might look like the mock-up below (courtesy of Brent).


In the tree above, two BOMs (say, "A" and "B") are compared. The green nodes with a "+" next to them represent nodes that were added (in "B" but not in "A") and the red nodes with a "-" represent nodes that were removed (in "A" but not in "B"). The blue nodes with the pencil represent nodes that are in both BOMs, but are different in some way (a.k.a. - mequal).

Now, there are many nodes that are exactly equals in both BOMs. It might sometimes be useful to show them, and it would look like the gray nodes below:


So, how do I go about identifying the nodes that are mequal to each other between the two BOMs? Well, it is not just a function of the two nodes in consideration, but also a function of the structure that they contain, and the structure that they are contained in. For example, if there is a panel (however these are identified) in the top-level of each BOM, then these would probably be considered to be mequal. But, if there are two panels in BOM "A" and only one in BOM "B", then there is a choice to be made: which panel in "A" is more mequal to the one in "B"? Answering this question may need to consider the structure (child nodes) of the panels being analyzed.

Whew! This seems like it will be hard work. So, I'll search for libraries that already implement it. Since a BOM is a tree structure that could be represented in XML, maybe an XMLDiff library exists that I can leverage. Let me search... yup! There are about a thousand and one XML diff libraries, but I couldn't find a maintained one that worked on unsorted nodes and didn't rely on strict node identity.

So, I search the research publications. I particularly like some of the ideas from this paper. I'll charge blindly forward and try to implement it. The next few blog posts will be about the implementation (if successful).

Fuggin Programming

WARNING: STRONG LANGUAGE AND BAD CODE

Hey, Folks! Blago here.
I'm programmin now! What, you didn't know I was doin that? Well, fuck you. I don't have much know-how under my belt yet, but I'm learnin this Scala shit that all the kids seem to be playin with. It's fuckin great. I mean, where else can I make a method name of "?<!#%^&*" and get away with it? The syntax looks just like I talk.

So, what can I code? What I know about is governing, so let me distill this knowledge down to a mini-quick how-to-govern trait:

 
trait Governance {

  type Favor
  type Promise
  type ShitIWant
  type Lobbyist
  type Bribe
  
  def solicit(favor: Favor)(lobbyist: Lobbyist): Bribe
  def pickBest(bribes: Seq[Bribe]): Bribe
  def accept(bribe: Bribe): Promise
  def collect(promise: Promise): ShitIWant
  
  def govern(lobbyists: List[Lobbyist], power: Seq[Favor]) = {
    for (favor <- power) yield
     collect(accept(pickBest(lobbyists.map(solicit(favor)))))
  }
  
}
 

I make it look easy, huh? Let's break it down now. The world of politics is made up of Lobbyists, Favors, Promises, and Bribes. Oh, and also shit-I-want. The whole point of all the other stuff is to get more shit-I-want.

So, let's look at the govern method. The inputs needed to govern are Lobbyists and Power. The Power gives you a steady stream of Favors that you can do for people, and you can keep that power as long as you *ahem* stay in office. Then, you got the Lobbyists. These fuckin pricks just want to get you to do favors for them for free. Don't be a dumbass, if you got somethin golden, make'em pay up the ass for it.

  def govern(lobbyists: List[Lobbyist], power: Seq[Favor]) = { ... }

How can you get the best deal for your Favors? Well, you can't just give it to the first asshole that comes along. You gotta shop it around. Get out your little black book and make some calls. This is illustrated in the solicit method

  def solicit(favor: Favor)(lobbyist: Lobbyist): Bribe

So you solicit your current Favor to every fuggin lobbyist you know, and try to get a Bribe from each of them. Then, you can compare them all to get the best one.

  def pickBest(bribes: Seq[Bribe]): Bribe

The best Bribe you can then accept, getting a Promise to pay up. You then collect on that Promise to get the ShitIWant, which is usually in the form of small unmarked bills (but not /that/ small).

  def accept(bribe: Bribe): Promise
  def collect(promise: Promise): ShitIWant

Notice that I'm usin what they call "abstract types" in this trait. That means that a type like "ShitIWant" could really be anything (like money), and needs to be defined by the implementing class.

What? You thought I was gonna implement the class myself and do all the work for you? Why don't you fuck yourself in the ear. Then, when you're done with that, go fuck yourself in the other ear. Then, come back and ask nicely, cause I'm not your fuckin jump-to-it kid.

Oh, all right. Since I'm such a nice guy, here's what a class might look like that extends my Governance trait.

 
object MyGovernance extends Governance {
  
  type Lobbyist = { def bribe(f: Favor): Bribe }
  type Favor = String
  case class Bribe(favor: Favor, amount: BigDecimal)
  case class Promise(bribe: Bribe)
  case class ShitIWant(amount: BigDecimal)
  
  def solicit(favor: Favor)(lobbyist: Lobbyist) = {
    lobbyist.bribe(favor)
  }
  
  def pickBest(bs: Seq[Bribe]) = {
    bs.foldLeft(Bribe("Nothing",0))((a,b)=> if(a.amount >= b.amount) a else b)
  }
  
  def accept(bribe: Bribe) = {
    Promise(bribe)
  }
  
  def collect(promise: Promise) = {
    ShitIWant(promise.bribe.amount)
  }
  
}
 

Notice that all those abstract types used to really be nothin more than names just floatin in space. But I had to tie them to something to implement the class. So, the "Favor" type is now just a type-alias for a String, so it could be something like "Pardon a rich man" or "Direct money to Project X". Other types, like Bribe, I defined directly.

So the jagoff implementing this class only needs to implement the component methods solicit, pickBest, accept, and collect. The basic structure of governing is already defined by me in the govern method, and it doesn't need any improvement. I heard some asshole talking about "idiomatic scala" and he said my code don't have it. Well, I told him that he must be an idiomatic because he didn't get any oxygen to his brain when he was in the womb and his mother was a whore.

But anyway, I can take constructive criticism. And, I started hearin about this shit called "composable functions". What's that? You just take some of these methods and plugem together to make new ones. You don't even need to define arguments and return types and shit like that, although the compiler will make sure you don't do anything stupid. Like, the place where I cherry-pick the best bribe and follow-through on it. In scala, I can define something like this:

  def cherryPick = pickBest _ andThen accept andThen collect

Lookit that. Now I got a new method that combines all those other methods together, but I can treat it like a single thing. Also, I can plug in the pieces of this thing in other ways to into other methods and treat them like lego building blocks. I love legos. Then, my govern method becomes more compact.

  def govern(lobbyists: List[Lobbyist], power: Seq[Favor]) = {
    for (favor <- power) yield
     cherryPick(lobbyists.map(solicit(favor)))
  }

If you were payin attention, you might be thinking that I could've saved a lot of trouble in defining all of those methods to plug together if I just would've defined the combined function from the start to implement at once:

  def cherryPick(bribes: Seq[Bribe]): ShitIWant

Then, you can implement it all at once and skip those pesky pickBest, accept, and collect methods:

  def cherryPick(bribes: Seq[Bribe]): ShitIWant = {
    val amt = bribes
      .foldLeft(Bribe("Nothing",0))((a,b)=> if(a.amount >= b.amount) a else b)
      .amount
    ShitIWant(amt)
  }

Whoah... slow down there, brother. I could have also just stubbed out the "govern" method and made you implement the whole fuckin thing. But, I'm tryin to supply a structure for you to base you implementation on. If you want to learn how to govern you better shuddup and pay attention. Not just the structure of the code I'm givin you is important, but also the semantics of the code. I took painstaking effort to name the types and variables so that you can understand the subtle meanings of all the players in this dance.

As a side note, the type names can (and should) be changed to reflect new meanings and realities. They are a communication tools just like code comments. But, also like comments, they can lie to you if you're lazy and let your code drift. For example, I recently found out that Lobbyists are not the only entity from which I can extract bribes. So, I should have refactored my code to include some super or genric type that includes Congressmen. So, if type/method/variable names are like comments and can lie to you. Maybe we should all just be using one-character variable names to at least limit the damage they can do. Then, the structure of the code pops out at you, unhindered by the story told by the names.

This guy obviously has mental problems:

After you have spent a certain amount of time in the compiler, you will
come to feel angry resentment at every comment you encounter, because it
might be trying to mislead you! I have modified my editor not to show me
any comments in scala sources so they cannot tempt me with their siren
songs of reasons and explanations. AH THE LIMITLESS SERENITY

Michael Feathers is all over this topic today on Tweeter. See if you can pick out the posts that matter from all of the other crap on there. I swear, people join Twatter because they think other people like the smell of their farts, then they stay because they start to like the fart-smell themselves. Fuggidaboutit.

The trade-off between names and structure appears to be constrained by ease-of-comprehension on one end and the need for reuse/composability on the other. Feathers considers that there are certain classes of code that are better understood in terms of their structure, effectively bridging the comprehension/composability divide.

Ha! He'll never get anything done if he keeps jackin around thinkin useless thoughts like that. Meanwhile, I just automated the entire process of executive governing. I'm ready for my next challenge to help the world... I think I'll make a web-framework in Java. That'll be fuckin Golden!

Stupid Emoticon Tricks

Just for giggles, I decided to see if could get emoticons to compile in Scala. Randomly picking from the Wikipedia page for Eastern-style emoticons, I find I can compile the following code:

package blevins.emoticon

object App extends Application {
  import Emoticon._
  
  val emoticons: List[Emoticon] =
    List( 
      ( ^ _ ^ ) ,
      ( ^ o ^ ) ,
      d ( ^ _ ^ ) b ,
      ( T _ T ) ,
      ( Z . Z )
    )
 
  for ( f <- emoticons ) { f.print }
}
 

It outputs the following:

(^_^)
(^o^)
d(^_^)b
(T_T)
(Z.Z)

The contents of the Emoticon object is left as an exercise for the reader. Note that I was unable to do the (-.-)Zzz emoticon, but maybe that is just because I didn't try hard enough.

If this doesn't convince you to return to Java, nothing will...

Shunting Yard Algorithm

So, the next JUG meeting is introducing the concept of a code kata. One suggestion for an example topic was the Shunting Yard Algorithm. I remember using an HP 42S RPN calculator all through school, and well into my professional life. So, I thought I'd give it a go.

Looking at the Wikipedia entry, they outline an algorithm in pseudo-english-code that can be implemented fairly easily in scala like this:

package org.okcjug.kata.shuntingyard

import scala.util.parsing.combinator._
import scala.util.matching.Regex
import scala.util.parsing.input.CharSequenceReader 
import scala.collection.mutable.Stack
import scala.collection.mutable.Queue

object ShuntingYardWikipediaParser extends RegexParsers {
  
  // the actual algorithm
  def rpn(s: String) = {
    val stack = new Stack[String]
    val queue = new Queue[String]
    
    for (t: String <- parseAll(tokens, new CharSequenceReader(s)).get) {
      
      if (t isNumber) { queue += t }
      if (t isOperator) { 
        while ((!(stack isEmpty) && (stack.top isOperator)) && (
               ((t isLeftAssociative) && (t isLowerOrEqualPrecedenceThan stack.top)) ||
               ((t isRightAssociative) && (t isLowerPrecedenceThan stack.top)))) {
          queue += stack.pop
        }
        stack push t
      }
      if (t isLeftParenthesis) ( stack push t )
      if (t isRightParenthesis) {
        while (!(stack.top isLeftParenthesis)) { queue += stack.pop }
        stack.pop
      }
    }
    while (!(stack isEmpty)) {
      if (stack.top isLeftParenthesis) { error("mismatched parens") }
      queue += stack.pop
    }
    queue.mkString(" ")
  }
  
  // definitions
  val number = """(\d+(\.\d+)?)""".r
  val product = """[\*\/]""".r
  val term = """[\+\-]""".r
  val exponent = """\^""".r
  val negation = """\!""".r
  val leftParens = """\(""".r
  val rightParens = """\)""".r
  val parens = leftParens | rightParens
  val token = number | product | term | exponent | negation | parens ^^ { case s: String => s }
  val tokens = token*
  
  // tricky implicit conversions to make the syntax prettier
  implicit def stringToSmartToken(s: String): SmartToken = { SmartToken(s) }
  case class SmartToken(s: String) {
    implicit def regexMatches(r: Regex): Boolean = { s.matches(r.toString) } 
    def isNumber: Boolean = number
    def isOperator = product || term || exponent || negation
    def isLeftAssociative = isOperator && ( product || term || negation )
    def isRightAssociative = isOperator && exponent
    def isLeftParenthesis: Boolean = leftParens
    def isRightParenthesis: Boolean = rightParens
    def precedence = {
      if (term) 1
      else if (product) 2
      else if (exponent) 3
      else if (negation) 4
      else error("Not an operator")
    }
    def isLowerPrecedenceThan(o: String) = {
      (s precedence) < (o precedence)
    }
    def isLowerOrEqualPrecedenceThan(o: String) = {
      (s precedence) <= (o precedence)
    }
  }
}
 

Note that I ignored the possibility of a function as described in the Wikipedia entry, but added the concept of a unary operator (negation, which I represent as a prefixed "!").

The interesting part of this starts at line 41, which has (through line 47) a bunch of regex definitions of the tokens to be read. Scala can convert a string to a regex using the ".r" method.

Lines 48 - 50 take the regular expressions and combine them into parsers combinators, which produce string tokens.

To make the string tokens syntactically pleasing, we implicitly convert them into a "SmartToken" (lines 53 - 75) which has methods relevant to this particular algorithm. Another interesting thing is line 55, which auto-magically converts a regex (defined in an outer scope) to be treated like a boolean value of that regex applied to the SmartToken's wrapped string. Yee-haw! A few more refactoring passes and it will look like Ruby while still allowing you to argue with the compiler over types.

But, I'll be honest. If I didn't find the Wikipedia description of the algorithm, I probably wouldn't have implemented it in the same way. Also, if I'm going to take the trouble to parse a language, I might as well build an abstract syntax tree.

Here is my elaborate AST model:

package org.okcjug.kata.shuntingyard

import scala.util.parsing.combinator._

abstract class Expression {
  def rpn: List[String]
}

case class NumberExpr(n: String) extends Expression {
  def rpn = List(n)
}

abstract class Operator extends Expression
case class UnaryOp(op: String, e: Expression) extends Operator {
  def rpn = e.rpn ::: List(op)
}
case class BinaryOp(op: String, l: Expression, r: Expression) extends Operator {
  def rpn = l.rpn ::: r.rpn ::: List(op)
}
 

And, I can parse it with this object:

package org.okcjug.kata.shuntingyard

import scala.util.parsing.combinator._
import scala.util.parsing.input.CharSequenceReader

object ShuntingYardParser extends RegexParsers {
   
  def expression(s: String) = parseAll(expr, new CharSequenceReader(s))
  def rpn(e: Expression) = e.rpn.mkString(" ")
  def rpn(s: String) = {
    val e = expression(s)
    if (e.successful) {
      e.get.rpn.mkString(" ")
    }
    else {
      error("Could not parse: " + s)
    }
  }
  
  // parser definitions
  def expr: Parser[Expression] = term 
  def num = """\d+(\.\d+)?""".r | failure("Some number expected")
  def number = num ^^ { case s => NumberExpr(s) }
  def group = "(" ~> expr <~ ")" ^^ { case e => e }
  def singular: Parser[Expression] = number | group | unaryOp | failure("Some expression expected")
  def unaryOp = "!" ~ singular ^^ { case s ~ e => UnaryOp(s, e) }
  def exponent = rightChain(singular, "^")
  def product = leftChain(exponent, "*"|"/")
  def term = leftChain(product, "+"|"-")
  
  // I think this is redundant, but couldn't figure out the chainx1(...) methods in scala's Parser class
  def rightChain(p: Parser[Expression], x: Parser[String]) = {
    ((p ~ x)*) ~ p ^^ {
      case Nil ~ tail => tail
      case rest ~ tail => rest.foldRight(tail) {
        case (p ~ s, z) => BinaryOp(s, p, z)
      }
    }
  }
  def leftChain(p: Parser[Expression], x: Parser[String]) = {
    p ~ ((x ~ p)*) ^^ {
      case head ~ Nil => head
      case head ~ rest => rest.foldLeft(head) {
        case (z, s ~ p) => BinaryOp(s, z, p)
      }
    }
  }

}
 

This code really does all the parsing definitions in lines 21 - 29. We produce an AST that can be output in RPN form.

The really tricky part (for me) about this code was defining it is such a way that we didn't get any recursive parsers as the first (leftmost) term of a sequential combination. This will lead to immediate stack-overflow purgatory as the parser infinitely recurses. Surprisingly, the compiler/type-checker allows it, and I've heard that it might be supported in a future implementation.

Well, do they work?

I guess we should actually test these implementations to see if they do what they are supposed to. Probably better even still to have defined some tests up front to allow the algorithm to be developed under that guidance. Scala has a wonderful testing facility called specs that allows you to specify test in a very intuitive way. Drop a library in my path and make some specifications>:

package org.okcjug.kata.shuntingyard

import org.specs._
import ShuntingYardParser._

object ShuntingYardTest extends Specification {
  
  def passStdTests(parser: { def rpn(s: String): String }) = {
    "be able to add and subtract" in {
      parser.rpn("3+4-2") must beEqual("3 4 + 2 -")
    }
    
    "do unary negation correctly" in {
      parser.rpn("! 3 + 2") must beEqual("3 ! 2 +")
      parser.rpn("!(3 + 2)^2") must beEqual("3 2 + ! 2 ^")
    }
    
    "parse Wikipedia example correctly" in {
      val input = "3 + 4 * 2 / (1-5) ^2 ^3"
      val result = parser.rpn(input)
      result must beEqual("3 4 2 * 1 5 - 2 3 ^ ^ / +")
    }
  }

  "ShuntingYardParser" should { 
    passStdTests(ShuntingYardParser)
  }
  
  "ShuntingYardParser" can { 
    "blow the stack" in {
      val sb = new StringBuffer
      val max = 1000
      for(i <- 1 to max) { sb append "(" }
      sb append "(4-3)"
      for(i <- 1 to max) { sb append "*(4-3))" }
      ShuntingYardParser.rpn(sb.toString) must throwA(new StackOverflowError)
    }
  }
    
  "ShuntingYardWikipediaParser" should {
    passStdTests(ShuntingYardWikipediaParser)
    
    "not blow the stack" in {
      val sb = new StringBuffer
      val max = 1000
      for(i <- 1 to max) { sb append "(" }
      sb append "(4-3)"
      for(i <- 1 to max) { sb append "*(4-3))" }
      ShuntingYardWikipediaParser.rpn(sb.toString) mustNot throwAn(new Exception)
    }
  }
}
 

This spec produces an executable class that produces this output:

Specification "ShuntingYardTest"
  ShuntingYardParser should
  + be able to add and subtract
  + do unary negation correctly
  + parse Wikipedia example correctly

  Total for SUT "ShuntingYardParser":
  Finished in 0 second, 0 ms
  3 examples, 4 expectations, 0 failure, 0 error

  ShuntingYardParser can
  + blow the stack

  Total for SUT "ShuntingYardParser":
  Finished in 0 second, 0 ms
  1 example, 1 expectation, 0 failure, 0 error

  ShuntingYardWikipediaParser should
  + be able to add and subtract
  + do unary negation correctly
  + parse Wikipedia example correctly
  + not blow the stack

  Total for SUT "ShuntingYardWikipediaParser":
  Finished in 0 second, 0 ms
  4 examples, 5 expectations, 0 failure, 0 error

Total for specification "ShuntingYardTest":
Finished in 0 second, 563 ms
8 examples, 10 expectations, 0 failure, 0 error

Notice that I'm testing both implementations of the parser with the same code, except for one test (blow the stack). This is because the AST version will blow up when it encounters some input that nests thousands of levels deep. I verify this and also verify that is doesn't affect the Wikipedia version. I'm am deeply embarrassed that a Wikipedia algorithm is more feature-full than my home-grown version.

What next?

Well, we could actually calculate the results of the input from either the AST or the rpn input. Both of these would be almost trivial to implement. We could randomly generate input strings, feed them into both parsers and compare the results. It is nice to have Scala's parser combinators as a tool in your belt. There is a dead zone between what can/should be done with one-off regular expressions, and generating a full-fledged language with an external tool (JavaCC, ANTLR, etc). Another option for these situations is to use an internal DSL (like the specs library I used). But, that's a topic for another post...

Disjoint Bounded Views - Redux

I cleaned up my previous post on "stuttering-or". The import would now look like this:

package org.okcjug.imports

class DisjointBoundedView[A,B](val a: Option[A], val b: Option[B])

object DisjointBoundedView {
  // namespace pollution?  Maybe use "||" or "OrType"
  type or[A,B] = DisjointBoundedView[A,B]
  
  // convenience of definition functions
  private def da[A,B](a: A): or[A,B] = { new DisjointBoundedView(Some(a),None) }
  private def db[A,B](b: B): or[A,B] = { new DisjointBoundedView(None,Some(b)) }
  private def na[A,B](n: Nothing): or[A,B] = { new DisjointBoundedView(None, None) }
  
  // implicit defs - stuttering-or
  implicit def noneToOr2[A,B](n: Nothing): or[A,B] =
    { na(n) }
  implicit def aToOr2[A,B](a: A): or[A,B] =
    { da(a) }
  implicit def bToOr2[A,B](b: B): or[A,B] =
    { db(b) }
  implicit def aToOr3[A,B,C](a: A): or[or[A,B],C] =
    { da(da(a)) }
  implicit def bToOr3[A,B,C](b: B): or[or[A,B],C] =
    { da(db(b)) }
  implicit def aToOr4[A,B,C,D](a: A): or[or[or[A,B],C],D] =
    { da(da(da(a))) }
  implicit def bToOr4[A,B,C,D](b: B): or[or[or[A,B],C],D] =
    { da(da(db(b))) }
  implicit def aToOr5[A,B,C,D,E](a: A): or[or[or[or[A,B],C],D],E] =
    { da(da(da(da(a)))) }
  implicit def bToOr5[A,B,C,D,E](b: B): or[or[or[or[A,B],C],D],E] =
    { da(da(da(db(b)))) }
  // more? ...

}
 

Calling code would look like this:

package org.okcjug.test

import org.okcjug.imports.DisjointBoundedView._

class Foo {

  def bar[T <% Int or String or Double](t: Option[T]) = {
    t match {
      case Some(x: Int) => println("processing Int: " + x)
      case Some(x: String) => println("processing String: " + x)
      case Some(x: Double) => println("processing Double: " + x)
      case None => println("empty and I don't care the type")
    }
  }
  
  def baz[T <% String or Int](t: List[T]) = {
    for (x <- t) x match {
      case x: String => println("String list item: " + x)
      case x: Int => println("Int list item: " + x)
    }
  }
}

object Foo extends Application {
  
  val f = new Foo
  
  f.bar(None)
  f.bar(Some(1))
  f.bar(Some("blah"))
  f.bar(Some(3.45))
  // f.bar(Some(Some(2))) // compiler error
  // f.bar(Some(Set("x", "y"))) // compiler error
  
  f.baz(List(1,1,2,3,5,8,13))
  f.baz(List("boogie", "woogie"))
  // f.baz(List(3.4, 3.14)) // compiler error
  // f.baz(List(1,"one")) // compiler error
  // f.baz(Some(1)) // compiler error
}
 

The only difference is that we now don't require clarifying the type for a None, and the class name more accurately reflects what it does.

UPDATE: Per Ittay's suggestion below, I've updated the implementation to use Either as the backing class (shown below). This simplifies the code and allows extraction of values from the composite type via pattern matching. Also, it can no longer accurately be described as "stuttering-or".

package org.okcjug.imports

object DisjointBoundedView { 
  // namespace pollution?  Maybe use "||" or "OrType"  
  type or[A,B] = Either[A,B]  
    
  // implicit defs 
  implicit def l[T](t: T) = Left(t)
  implicit def r[T](t: T) = Right(t)
  implicit def ll[T](t: T) = Left(Left(t))
  implicit def lr[T](t: T) = Left(Right(t))
  implicit def lll[T](t: T) = Left(Left(Left(t)))  
  implicit def llr[T](t: T) = Left(Left(Right(t))) 
  implicit def llll[T](t: T) = Left(Left(Left(Left(t))))  
  implicit def lllr[T](t: T) = Left(Left(Left(Right(t))))  
  // more? ...  
    
}

OKCJUG Slides

Although they may not make much sense without the code and explanation that goes along with them, I've posted the slides used in my JUG presentation yesterday.

Stuttering Or

So I read both Jim McBeath and Michid's blog entries on implementing polymorphism using implicit conversions, especially where it would be otherwise difficult because of type erasure. But, I was uneasy with their approaches. Jim's required implementing redundant classes in a heirarchy and Michid's seemed comlex. Both required that you explicity implement an implicit function for each disjoint type you want one of your method's parameters to be called as. And, even worse, the calling code has to remember to import the implicit functions for this to work.

I call my attempt at a better version the "stuttering-or" method, and it looks like this:

package org.okcjug.typeerasure.arrrgh.util

case class DisjointType[A,B](val a: Option[A], val b: Option[B])

object DisjointType {
  type or[A,B] = DisjointType[A,B] // who wants to type "DisjointType" all the time?
  
  // convenience of definition functions
  private def da[A,B](a: A): or[A,B] = { DisjointType(Some(a),None) }
  private def db[A,B](b: B): or[A,B] = { DisjointType(None,Some(b)) }
  
  // implicit defs - stuttering-or
  implicit def aToDisjointType2[A,B](a: A): or[A,B] =
    { da(a) }
  implicit def bToDisjointType2[A,B](b: B): or[A,B] =
    { db(b) }
  implicit def aToDisjointType3[A,B,C](a: A): or[or[A,B],C] =
    { da(da(a)) }
  implicit def bToDisjointType3[A,B,C](b: B): or[or[A,B],C] =
    { da(db(b)) }
  implicit def aToDisjointType4[A,B,C,D](a: A): or[or[or[A,B],C],D] =
    { da(da(da(a))) }
  implicit def bToDisjointType4[A,B,C,D](b: B): or[or[or[A,B],C],D] =
    { da(da(db(b))) }
  implicit def aToDisjointType5[A,B,C,D,E](a: A): or[or[or[or[A,B],C],D],E] =
    { da(da(da(da(a)))) }
  implicit def bToDisjointType5[A,B,C,D,E](b: B): or[or[or[or[A,B],C],D],E] =
    { da(da(da(db(b)))) }

}
 

The "magic" part of this is that it allows infix type notation to represent "Type1 or Type2" as "DisjointType[Type1,Type2]". Then, the implicit defs allow the component types to be represented in a type view. This guards the methods that define it to only accept members of the component types. Note that it is up to the method implementer to cover all the possible cases as the type system will not help you there.

Defining the methods is something like this:

package org.okcjug.typeerasure.arrrgh.work

import org.okcjug.typeerasure.arrrgh.util.DisjointType._

class Foo {

  def erasureMethod[T <% Int or String or Double](t: Option[T]) = {
    t match {
      case Some(x: Int) => println("processing Int: " + x)
      case Some(x: String) => println("processing String: " + x)
      case Some(x: Double) => println("processing Double: " + x)
      case None => println("empty and I don't care the type")
    }
  }
  
  def erasureMethod2[T <% String or Int](lt: List[T]) = {
    for (x <- lt) x match {
      case x: String => println("String list item: " + x)
      case x: Int => println("Int list item: " + x)
    }
  }
  
}
 

And, the calling code looks like this:

package org.okcjug.typeerasure.arrrgh

import org.okcjug.typeerasure.arrrgh.work.Foo
import org.okcjug.typeerasure.arrrgh.util.DisjointType._

object App extends Application {

  val f = new Foo()
  
  f.erasureMethod(Some("blah"))
  // f.erasureMethod(None) // compiler error
  f.erasureMethod(None.asInstanceOf[Option[String]]) // ok
  f.erasureMethod(Some(42))
  // f.erasureMethod(Some(List("b"))) compiler error
  
  f.erasureMethod2(List("a","b","c"))
  f.erasureMethod2(List(5,4,3,2))
  // f.erasureMethod2(List(4.3)) compiler error

}
 

So, what does this get me? Well, implementing the code is fairly straightforward, just using a "Type1 or Type2 or Type3 ..." construct for the disjoint types (up to 5 in the given code). Also, discerning the specific type within the polymorphic method for purposes of dispatch is done using the standard "match" keyword.

What I don't like about my solution is that the calling code must import the implicit methods (here: org.okcjug.typeerasure.arrrgh.util.DisjointType._). Each of the the compared methods from the top of this article also required importing the implicit methods. However, I think my approach shows more promise because the implicit defs that need to be imported are not specific to the pseudo-polymorphic methods I'm implementing. In fact, the content of this import is suitable to be included in the Predef object.

Maybe I'll poke around the scala mailing list and see if any library maintainers want to oblige me...

Lazy initialization of blog posts

Well, it has been a couple of years since my last post and we did not get the opportunity to use Scala at work. I lost interest and started chasing other shiny, twinkly things.

But, I did get a chance to give a presentation on Scala at the local JUG. I'll post slides when it is done if I don't completely embarrass myself.